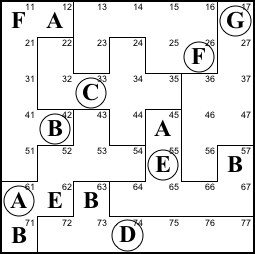
Du-Sum-Oh Solving Tutorial
Below is the puzzle we want to solve. We need
to place the letters A-G in the cells so that each row contains
exactly one of each letter. Ditto for each column and for each
region. Several letters have been given to start us off.
This tutorial refers to rows and columns by number,
and to regions by the starter letter in the region.

Step 1. Column 1 and region B share the
five purple cells below left. Thus the two pink cells that
complete column 1 and the two blue cells that complete region
B must contain the same two symbols. So cell 12 must
be A and cell 71 must be B. The result is shown below right.
12=A, 71=B


Step 2. Similarly, row 7 and region D
share the six purple cells below, so the pink cell (which
completes region D) must be the same as the blue cell (which
completes row 7).
63=B


Step 3. Row 1 and region F and share
the four purple cells, so the three pink cells must contain the same
symbols as the three blue cells. The pink cells already
contain A and G, so they must pick up the F from 26
to fill 11. 23 and 25 will eventually be A and G but we
can't yet determine which is which.
11=F


Step 4. Comparing row 6 and region E
we see that the three blue cells must be the same as the three pink cells.
They must contain A, B, and E, so the pink cells need
E in 62. The blue cells need an A and a B, but row 5
already has B, so 45 is A. That leaves B for 57.
This can be described as the little law of
leftovers. Wherever a region overlaps a row or column,
the parts outside the overlap (the leftovers) have to be the
same.
E=62, 45=A, 57=B

Step 5. Row 5 and region A reveal
that the pink cells must contain A, B, E, and something
else. Column 1 has an A so 51 can't be A. The A must
be at 56.
Even though we don't yet know what the "something
else" is, we know that cells 43 and 51 are the same.
This knowledge could help us (though in this puzzle it
isn't needed).
56=A


Step 6. Column 7 and region G reveal that the pink cells need
B and the blue cells need A. 46 can't be B (due to 42)
so 36 is B. And 67 can't be A (due to 61) so 77 is A.
36=B, 77=A


Step 7. We have now assigned five As; there are only two
left. They have to be in rows 2 and 3 and columns 3 and
4, the purple cells. The only possibility that
keeps them in a different row and column is 23 and 34.
And looking again at row 1/region F (as we did in step
3), we see that 25 is G.
23=A, 34=A, 25=G


Step 8. We have also assigned five Bs; the two left
must be in the purple cells, so they must be
14 and 15.
24=A, 15=A


Step 9. Consider region C. It lacks D, E, F, and G.
Columns 2 and 5 contain E, the 44 is E. The G at 25
kills the possibility of G at 22 and 35, so 32 is G.
The F in row 2 forces the F to 35. And the only place
left for the D is 22.
44=E, 32=G, 35=F, 22=D.


Step 10. Column 5 lacks C and D. The D at 74 forces 75 to
C and 65 to D.
75=C, 65=D


Step 11. Similarly, column 2 lacks C and F, and the C at 75
forces 72 to F and 52 to C.
72=F, 52=C


Step 12. Row 1 lacks C, D, and E. Column 4 already contains
D and E, so 14 is C.
forces 72 to F and 52 to C.
14=C


Step 13. Rows 2 and 3 and column 6 contain F, so the only spot
left for an F in region G is 47.
47=F


Step 14. Row 6 lack C, F, and G. The Fs at 26 and 47 force
F to 64. Then the G at 17 forces G to 66 and C to 67.
64=F, 66=G, 67=C


Step 15. Column 7 gets D in 37 (due to D in 22) and E in 27.
This allows us to finish off row 2 with C at 21, row 3 with
E at 31, and region G with C at 46.
37=D, 27=E, 21=C, 31=E, 46=C


Solution. At this point things easily
fall in place.
54=G, 76=E, 16=D, 13=E, 43=D, cell 53=F, 73=G, 51=D, 41=G

Back to Bob’s main Du-Sum-Oh page.