Du-Sum-Oh Solving Tutorial
Below is the puzzle we want to solve. We need
to place the letters A-H in the cells so that each row contains
exactly one of each letter. Ditto for each column and for each
region. Several letters have been given to start us off.
This tutorial refers to rows and columns by number,
and to regions by the starter letter in the region.
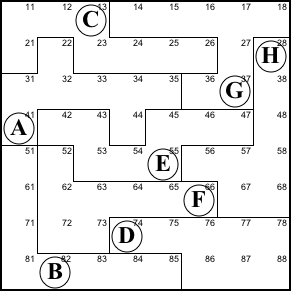
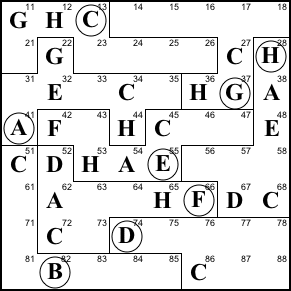
Step 1. Rows 1, 2, and 3 share the 22
purple cells below left with regions A, C, and G. The columns
have the to extra pink cells, while the regions have the two
extra blue cells. Both the regions and the rows have three
full sets of letters. So whatever is in the two pink cells
must be the same as what's in the two blue cells.
So 44 is H and 38 is A.
This the big law of leftovers. Wherever
a group of regions overlaps some rows or columns, the parts
outside the overlap (the leftovers) have to be the same.
44=H, 38=A
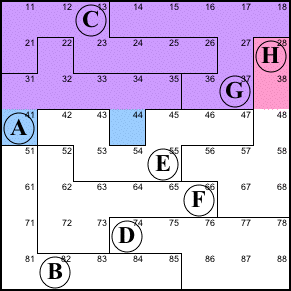
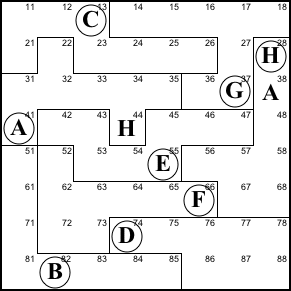
Step 2. Using the big law of leftovers
again, we see that 22 is G and 36 is H.
22=G, 36=H
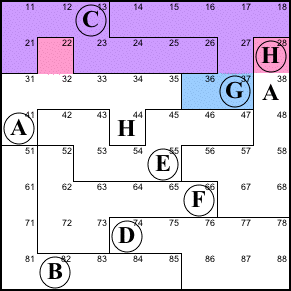
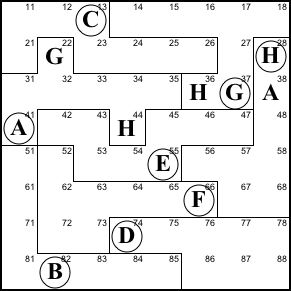
Step 3. The little law of
leftovers is a special case of the big law, applied
to a single region and row/column. Here we see the blue
and pink cells must both contain C, H, and G. 27 is C,
and the G at 22 forces the pink G to 11 and H to 12.
27=C, 11=G, 12=H
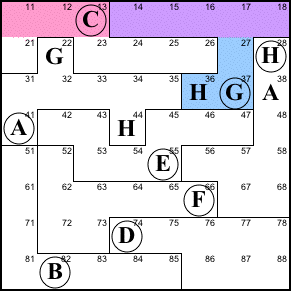
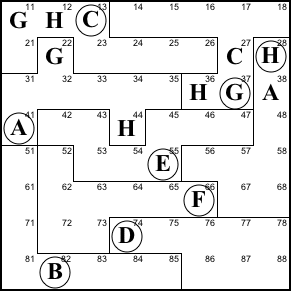
Step 4. The big law of leftovers
shows that 48 is E, 53 is H (because the H at 44 prevents
54 from being H) and 54 is A.
48=E, 53=H, 54=A
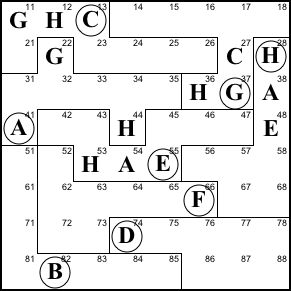
Step 5. Region F lacks an H. Columns
2, 3, and 4 already have H, so the only place remaining is
65.
65=H
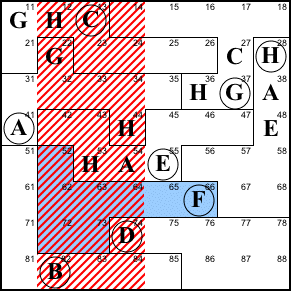
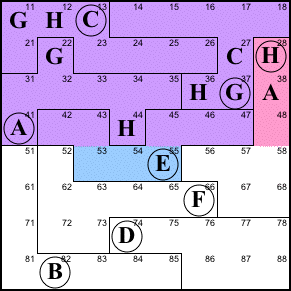
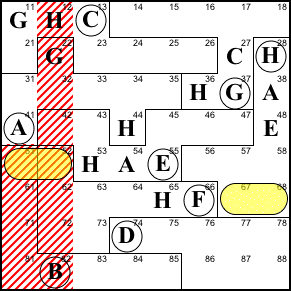
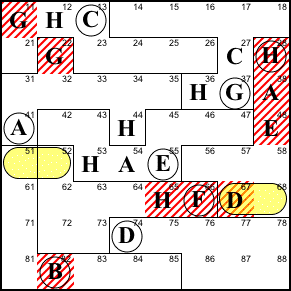
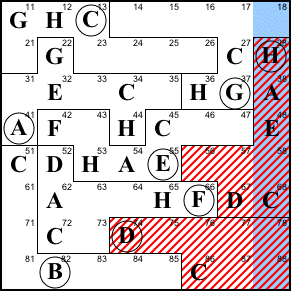
Step 6. This is the most complicated
step in the solution. The big law below, top left) shows
us that 51 and 52 contain the same thing as 67 and 68,
without indicating which matches up with which.
The B at 82 prevents either 51 or 52 from being
B (below, top right). Thus neither 67 nor 68 can be B.
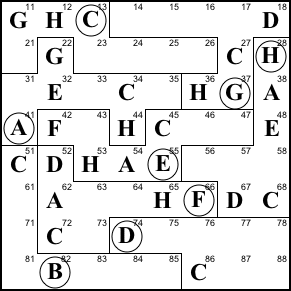
67 cannot be A, B, C, E, F, G, or H (below, bottom
left), because its region already contains A, E, and H, its
column contains C and G, its row contains F, and we just
established it can't be B. Thus it has to be D.
67=D
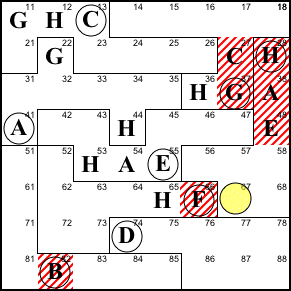
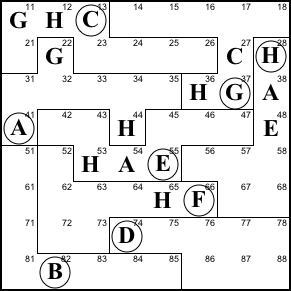
Step 7. Neither 51 nor 52 can be a
G because of the two Gs in columns 1 and 2. So 68 can't
be G and for reasons similar to step 6, the only thing it
can be is C.
68=C
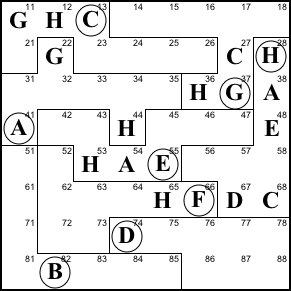
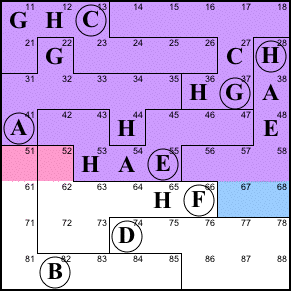
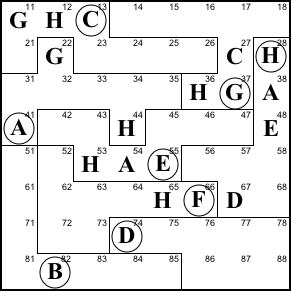
Step 8. The only place in region
F that can still be D is 52. And since 51+52=67+68, 51
must be C.
52=D, 51=C
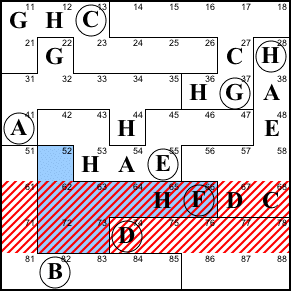
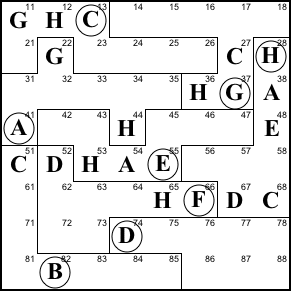
Step 9. The little law says one
of the blue cells must be C. But columns 7 and 8 already
have C, so the C must be in 86.
86=C
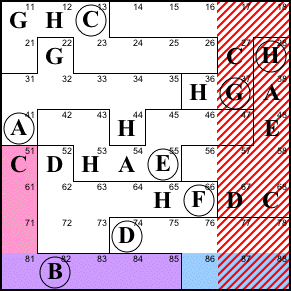
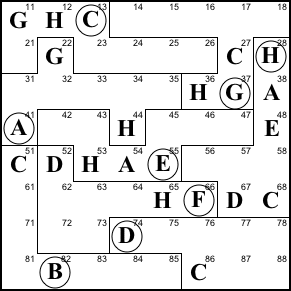
Step 10. Row 7 needs a C, but 71
can't be C because of the C in region B; 73 can't be C
due to the C in column 3; and 74 thru 78 are killed by
the C in region D. So 72 is C.
This gives us 6 of the 8 Cs. The remaining two
have to be at 34 and 45.
72=C, 45=C, 34=C
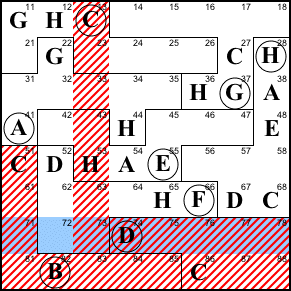
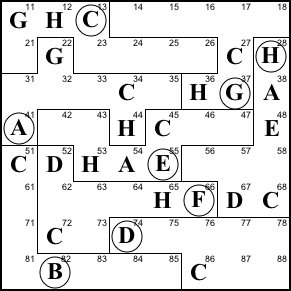
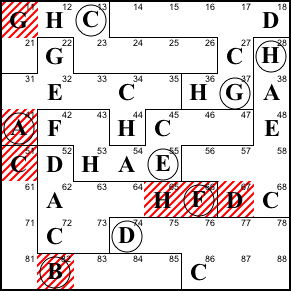
Step 11. Column 2 lacks A, E, and F.
Row 4 already contains A and E, so 42 is F. Then the A
in row 3 means 32 is E, and 62 is A.
42=F, 32=E, 62=A
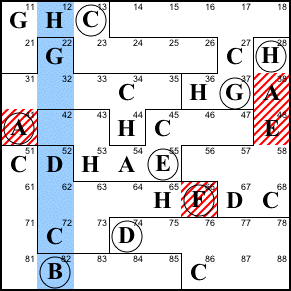
Step 12. The only place left for
D in column 1 is 18.
18=D
Step 13. The only possibility for
61 is E.
61=E
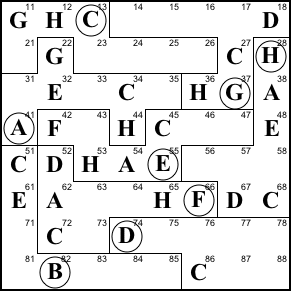
Step 14. Column 7 lacks A, B, E,
F, and H. As a member of row 4 and region E, 47 cannot
be A, E, F, nor H, so it must be B. 57 can't be A, E,
nor H (row 5) so it must be F.
The little law says 51+61+71 = 86+87+88. So
87 or 88 must be an E. But column 8 already has an E,
so the E is 87.
That leave the A and H. 17 can't be H because
region G already has H. So 17 is A and H is at 77.
47=B, 57=F, 87=E, 17=A, 77=H
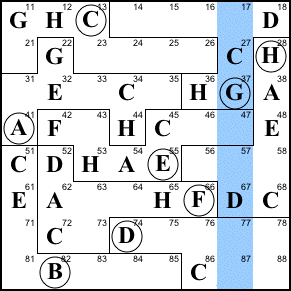
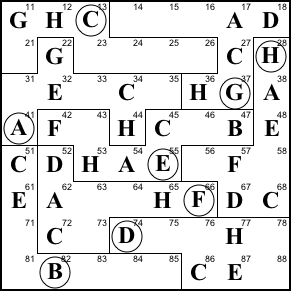
Step 15. We've place 7 Hs, so the
last one is at 81.
81=H
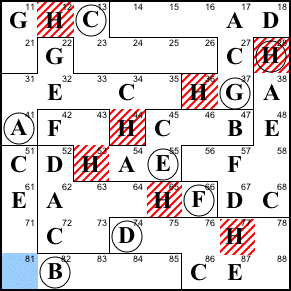
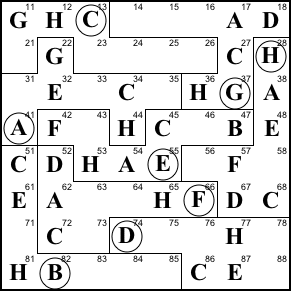
Step 16. 71 can only be F. And the
little law (51+61+71 = 86+87+88) says 88 is also F.
71=F, 88=F
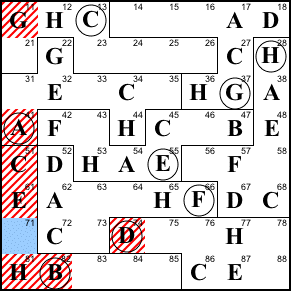
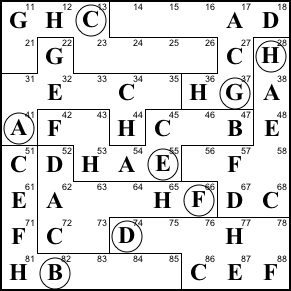
Step 17. 84 can only be G.
84=G
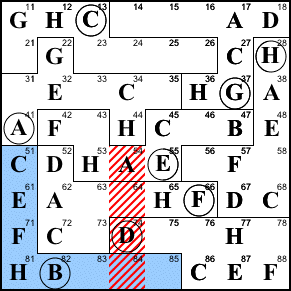
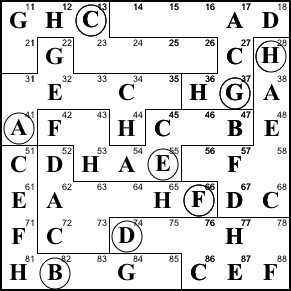
Step 18. We can finish off
region F by filling in B, E, and G in the only
possible spots.
64=B, 63=G, 73=E
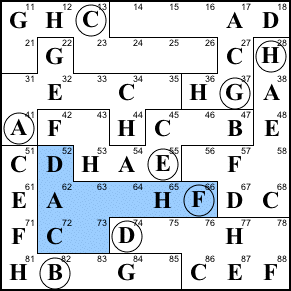
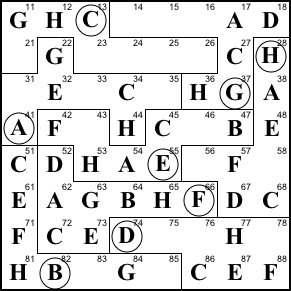
Step 19. Finish row 4.
43=D, 46=G
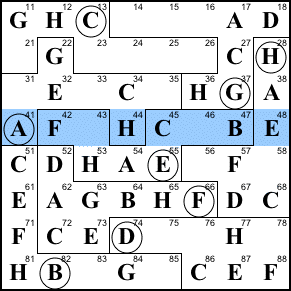
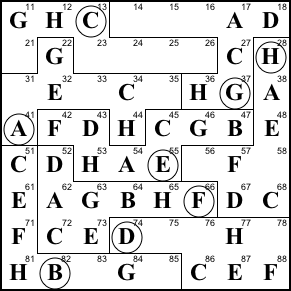
Step 20. Finish regions
B and H.
56=B, 58=G, 83=A, 85=D
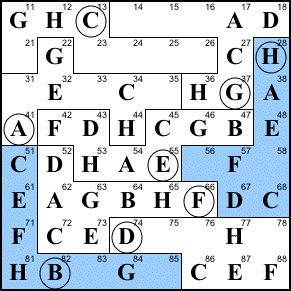
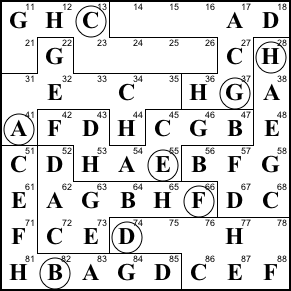
Step 21. Finish row 7 and
region G.
16=E, 14=F, 15=B, 78=B, 76=A, 75=G
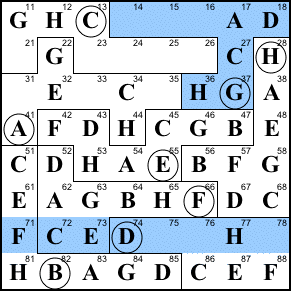
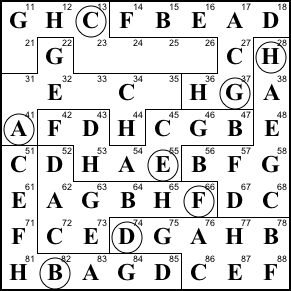
Step 22. Finish column 6
and region A.
26=D, 35=F, 33=B, 31=D
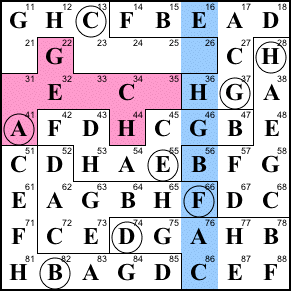

Solution. Finish row 2, and
the puzzle is complete.
21=B, 23=F, 24=E, 25=A

Back to Bob’s main Du-Sum-Oh page.