Tenpenny
I came up with Tenpenny back in the early 1980s. It appeared in Michael
Keller’s
World Game Review,
and then apparently got some play and discussion in the British magazine
Games and Puzzles (though I never got to see this).
The motivation for the game was the discovery of colored labels that are just
about the same size as a U.S. penny. These labels can be found in any office
supply store in the U.S. The pennies can be found in your pocket.
Rules:
You have ten pennies with the sides colored with five different
colors, every possible pair of colors occurring once. One player (the
constructor) secretly removes one of the pennies, then arranges the other
nine on the table in front of you. Initially you can only see the top side
of each penny. Alternatively, you can act as your own constructor by mixing
up the coins in your pocket, grabbing all but one, and (without looking),
tossing them on the table.
Your goal is to figure out which penny is missing, in as few ‘turns’
as possible. A turn consists of picking up a penny and looking at its bottom
side.
Example:
The five colors are
 red
red
 green
green
 blue
blue
 orange
orange
 yellow
yellow
Initially you see three reds, two greens, one blue, two oranges, and one
yellow:
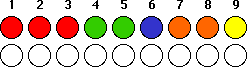
You flip coin number 4 and note that the bottom side is blue. Then you flip
coin 5 and find red underneath. So now you know:
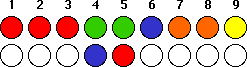
Since you have seen all four reds, you will not need to flip coins 1, 2, or 3.
You know they have blue, orange, and yellow underneath (and you don’t
care which is which). You then flip coin 9 and find green; you now have:
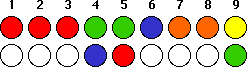
You’ve now seen three of the greens. The only green still unaccounted
for is green/orange, so you try coin 7. You’re hoping to find green but
instead find yellow:
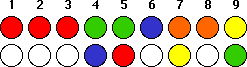
You now flip coin 6 and find orange:
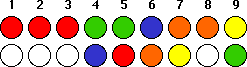
At this point, two coins are still unaccounted for— green/orange and
blue/yellow. So coin 8 must be green/orange and the missing coin is
blue/yellow.
Questions:
- If you see
 , what coin turning
strategy gives you the fewest expected turns to a solution? Assume that any
missing coin (that is consistent with this pattern) is equally likely.
, what coin turning
strategy gives you the fewest expected turns to a solution? Assume that any
missing coin (that is consistent with this pattern) is equally likely.
- Is there any initial combination you would see that would allow you to
identify the missing coin without taking any turns?
- What is the optimal strategy for the constructor, so that you will take
the largest number of expected turns to identify the missing coin?
Back to Bob’s main Game Ideas page.
 , what coin turning
strategy gives you the fewest expected turns to a solution? Assume that any
missing coin (that is consistent with this pattern) is equally likely.
, what coin turning
strategy gives you the fewest expected turns to a solution? Assume that any
missing coin (that is consistent with this pattern) is equally likely.
 red
red
 green
green
 blue
blue
 orange
orange
 yellow
yellow




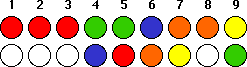
 , what coin turning
strategy gives you the fewest expected turns to a solution? Assume that any
missing coin (that is consistent with this pattern) is equally likely.
, what coin turning
strategy gives you the fewest expected turns to a solution? Assume that any
missing coin (that is consistent with this pattern) is equally likely.