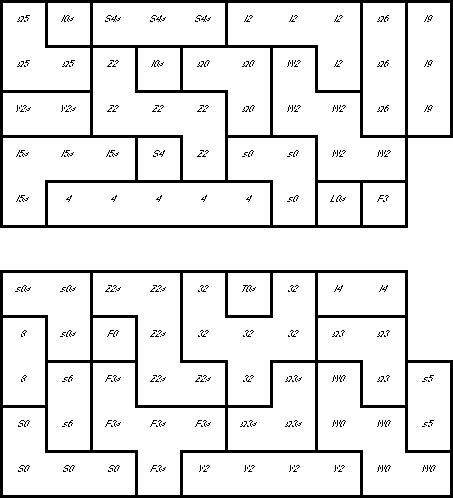
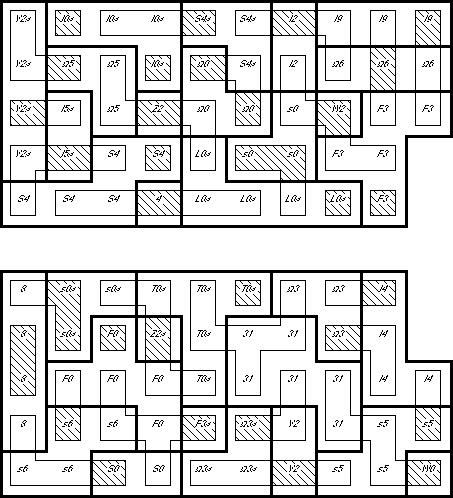
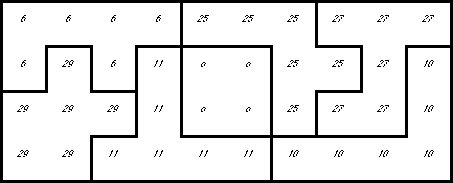
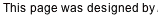The diagrams below are a map of a solution to packing the 166 hexacubes into a
10x10x10 cube. Since the hexacube set has a total volume of 996, a square
tetracube has been placed in the center of the top face to complete the cube.
This solution is partitioned into ten identical slabs, plus a plank. The
4x10x1 plank is centered in the top layer of the cube. The slabs are each
5x10x2, with a 2x2x1 chunk removed from the corner. The slabs can be arranged
in 10! orders, and the upper plank can be flipped over; this represents over 7
million different solutions.
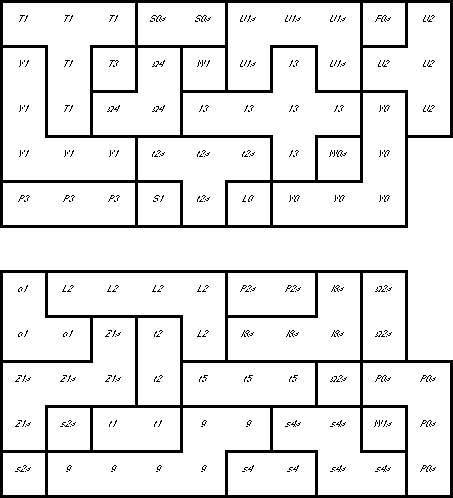
How to Read the Map: The heavy outlines show the piece borders on each layer.
The thin outlines show the piece borders on the next higher layer.
Crosshatching shows a vertical connection between those layers. Since no piece
occupies more than two layers, the outlines and crosshatching are enough to
completely describe a piece. As an additional aid, the
non-standard piece names (of the piece in the
current layer) are included in each location.
4x10x1 plank
Slabs 1 and 2

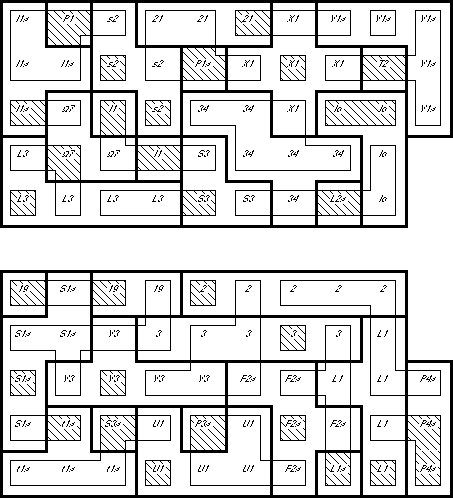
Slabs 3 and 4
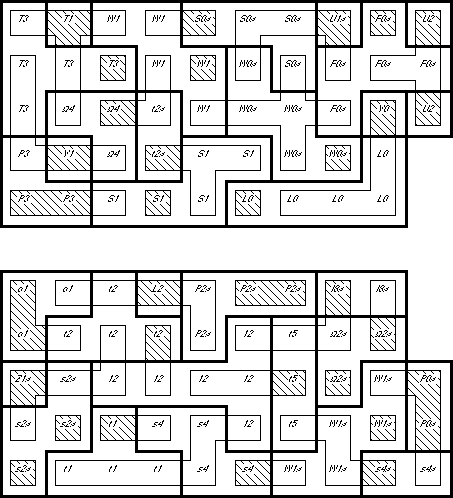
Slabs 5 and 6

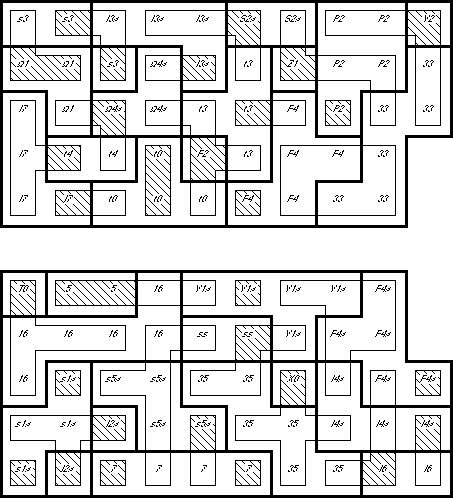
Slabs 7 and 8
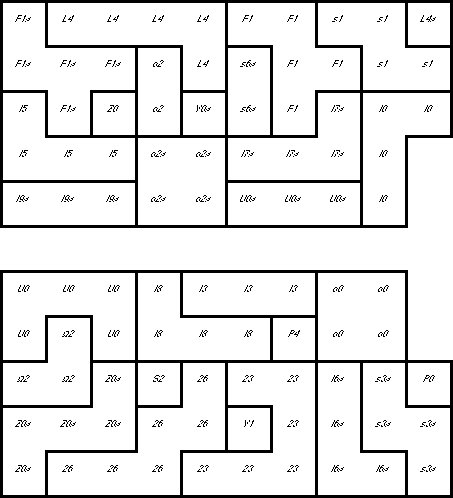
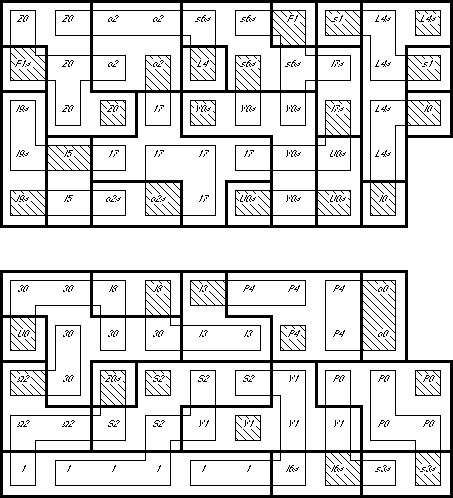
Slabs 9 and 10