Can you help Cubber D. Bear set up Christmas lights on his roof, so Santa won't miss his house? Cubber wants to set them up the same as last year, but has forgotten which string goes where.

He wants a string of lights in each marked region, and wants each row to have one light of each color. Ditto for each column.

Cubber remembers where one light of each color should go, and you must match those lights as you place the strings.

For a harder challenge, try to place all the lights without looking at the strings. Make sure that each region has a light of each color, just like the rows and columns do.

           
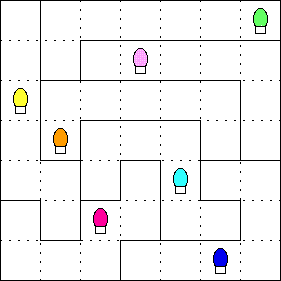
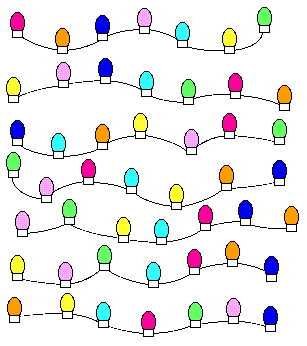
The goal is to place one string of lights in each region. Each string contains one light of each color. The same is to be true of each row and column.

Consider the region that has a green bulb () at one end. Three strings have a green bulb on an end, so one of these strings must be used in this region. But using the top string there would put a purple bulb () in the middle column. That column already has a purple bulb, so you can't use that string in this region.

Use similar logic to try to find a string that must go in a particular region. Placing that string will then eliminate possibilities for other strings elsewhere.

It is possible to solve the puzzle without looking at the strings. For example, the third row (from the top) must have an orange bulb () in the far right column. Why? Because the rest of the row belongs to a region that already has an orange bulb. Similar logic will allow you to fill in all the other lights.

Information about this puzzle (a Latin Squares Puzzle)
Solution Guide (using strings) (this walks you step by step to the solution)
Solution Guide (without strings) (this walks you step by step to the solution)

What is Cubber D. Bear's middle name?

Solution (don't look if you don't want to see the solution!)